Summary: In this tutorial, we will learn what the Merge Sort Algorithm is, how it works, and how to sort an array using the Merge Sort algorithm in Python, C, and Java.
Introduction to Merge Sort Algorithm
Merge sort is a divide and conquer algorithm that divides the array repeatedly into equal halves and arranges them accordingly in the merge process.
Here is the visualization of how merge sort works:
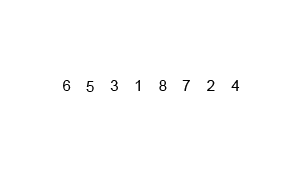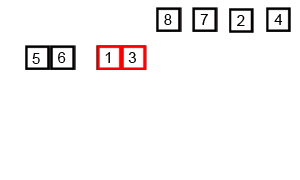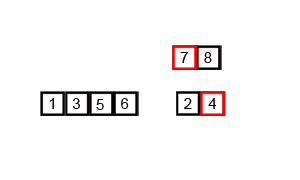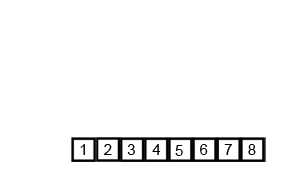
The algorithm first iteratively divides the array into equal partitions until each partition reduces to a single element.
Then it combines them in the same manner as they were divided in an ordered way.
Merge Sort Algorithm
- Partition the array into equal halves.
- Repeat step-1 for both left and right partitions, until the partition reduces to only one element.
- Merge the partitions into the original array in sorted order.
- Repeat step-3 until all the partition is merged.
In actual programming, we don’t merge the partitions (sub-arrays) into a new array or list rather we implement the divide and merge process on the original array using recursion.
The base condition of the recursion i.e. start_index<end_index ensures that the dividing process stops if the partition has a single element.
Here is the implementation of the steps in C and Java:
Python
class MS:
@staticmethod
def divide(arr, s, e):
''' Method to virtualy divide
array into equal halves'''
if s>=e:
return
m = (s+e)//2
MS.divide(arr, s, m)
MS.divide(arr, m+1, e)
'''call the merge funtion to sort'''
MS.merge(arr, s, m, e)
@staticmethod
def merge(arr, s, m, e):
''' Method to sort the
virtually divided partirions '''
'''copy values of partitions into
different arrays '''
n1 = m-s+1
n2 = e-m
a1 = []
a2 = []
for i in range(n1):
a1.append(arr[s+i])
for j in range(n2):
a2.append(arr[m+1+j])
'''orderly fill the original array with
the values of two new arrays '''
i=0
j=0
k=s
while i<n1 and j<n2:
if a1[i] < a2[j]:
arr[k] = a1[i]
i = i+1
else:
arr[k] = a2[j]
j = j+1
k = k+1
''' fill the left out elements '''
while i<n1:
arr[k] = a1[i]
k = k+1
i = i+1
while j<n2:
arr[k] = a2[j]
k = k+1
j = j+1
if __name__ == '__main__':
arr = [12, 35, 87, 26, 9, 28, 7]
MS.divide(arr, 0, len(arr)-1)
print(arr)C
#include <stdio.h>
#include <stdlib.h>
//Funtion to display array
void display(int a[], int size){
for(int i=0;i< size;i++){
printf("%d ",a[i]);
}
printf("\n");
}
void merge(int a[], int s, int m, int e){
int n1 = m-s+1, n2 = e-m;
int a1[n1], a2[n2];
int i, j, k;
for(i=0; i<n1; i++){
a1[i] = a[s+i];
}
for(j=0; j<n2; j++){
a2[j] = a[m+1+j];
}
i=0; j=0; k=s;
while(i<n1 && j<n2){
if(a1[i] < a2[j])
a[k++] = a1[i++];
else
a[k++] = a2[j++];
}
//Appending any left element of a1[]
if (i < n1){
for( ; i<n1; i++){
a[k++]= a1[i];
}
}
//Appending any left element of a2[]
if (j < n2){
for( ; j<n2; j++){
a[k++]= a2[j];
}
}
}
void mergeSort(int a[],int s,int e){
int m;
if(s<e){
m= (s+e)/2;
//Divide
mergeSort(a, s, m);
mergeSort(a, m+1, e);
//Merge
merge(a, s, m, e);
}
}
int main()
{
int a[] = {12, 35, 87, 26, 9, 28, 7};
printf("Unsorted array \n");
display(a,7);
//sorting
mergeSort(a, 0, 6);
printf("Sorted array \n");
display(a,7);
return 0;
}Java
public class MergeSort {
int a[];
public MergeSort(int[] a) {
this.a = a;
}
public void sort(int a[], int s, int e){
int m;
if(s<e){
m = (s+e)/2;
//Divide
sort(a, s, m);
sort(a, m+1, e);
//Merge
merge(a, s, m, e);
}
}
private void merge(int[] a, int s, int m, int e) {
int n1 = m-s+1, n2 = e-m;
int a1[] = new int[n1];
int a2[] = new int[n2];
int i, j, k;
for(i=0; i<n1;i++){
a1[i] = a[s+i];
}
for(j=0; j<n2;j++){
a2[j] = a[m+1+j];
}
i=0; j=0; k=s;
while(i<n1 && j<n2){
if(a1[i] < a2[j]){
a[k++] = a1[i++];
else
a[k++] = a2[j++];
}
//Appending if any element left in the a1[]
if (i < n1){
for( ;i<n1;i++){
a[k++]= a1[i];
}
}
//Appending if any element left in the a2[]
if (j < n2){
for( ;j<n2;j++){
a[k++]= a2[j];
}
}
}
}
public class App {
public static void main(String args[]){
int a[] = {12, 35, 87, 26, 9, 28, 7};
MergeSort ms = new MergeSort(a);
System.out.print("Unsorted array \n");
display(a);
//sorting
ms.sort(a, 0, 6);
System.out.print("Sorted array \n");
display(a);
}
private static void display(int[] a) {
for(int i=0;i< a.length ;i++){
System.out.print(a[i]+" ");
}
System.out.println();
}
}Output
Unsorted array 12 35 87 26 9 28 7 Sorted array 7 9 12 26 28 35 87
In the above program, the recursive function sort() or mergeSort() do the work of dividing the array and the merge() function arranges the elements of the partitions in sorted order.
In the merge function, we use extra two arrays a1 and a2 to store the array values of the left and right partition. We then put these array values one by one into the original array in an ordered fashion.
Overview of Merge Sort
- Not an in-place algorithm: Requires two extra arrays for splitting into two halves.
- O(Nlog2N) complexity: We are repeatedly dividing the array.
- Stable algorithm: No interchange of duplicated values.
In this tutorial, we learned what the merge sort algorithm is, how it works, and how to implement it to sort an array in C, Python, and Java programming languages.
